こんにちは、ジェノンです。
前回まで、車やミニ四駆の速度や加速度の計算方法を解説しました。
速度計算の回ではスピード重視のマシンが圧勝でしたが、前回の加速度の話題ではスピードを重視しすぎたために加速が遅くなってしまい、スタートで出遅れてしまっていましたね。
今回はそんな、「スタートに出遅れたスピード重視のミニ四駆は、加速重視のマシンをいつ追い越す事ができるか」を計算してみたいと思います。
よろしくお願いします。
この記事について
この記事で分かる事
- 等速直線運動する物体の、時間ごとの移動距離を求める。
- 等加速度直線運動する物体の、時間ごとの移動距離を求める。
こんな人に向けて書いています
- スタートで出遅れたスピード重視のマシンが追い越すまでの考え方を知りたい。
- ミニ四駆でスピード重視か加速重視かを検討するヒントが欲しい。
この記事の対象目安:高校生以上
高校生以上で習うことが含まれているので対象目安を高校生以上としましたが、極力ミニ四駆をやっている中学生にも分かるように頑張ります。
この記事の結論
計算条件
直線のコースとする。(コーナーによる減速を考えない、直線運動)
全ての抵抗は無視し、タイヤと路面との摩擦係数は1(滑らない)とする。
最高速度の計算は、モータ回転数、ギヤ、タイヤ直径から導かれる速度とする。
加速度は、モータトルク、ギヤ、タイヤ直径、マシン質量から加速度求め、最高速度に達するまで一定の加速度を保つ(等加速度直線運動)ものとする。
計算方法
移動距離L=加速中に移動した距離L1+等速で移動した距離L2
スタートからの時間をt、スタートから最高速度に達するまでの時間をtcとすると、
L=(1/2)×V×t=(1/2)×a×t^2 (但し、t < tc)
L=(1/2)×V×tc + V×(t-tc) (但し、t ≧ tc)
加速重視マシンの移動距離Laより、スピード重視マシンの移動距離Lbが大きくなった時の時間tが、追い越した時間となる。
実はリアルな値を求めるのは結構難しいという話
今回の問題の解説を行う前の補足事項として、リアルな現象を捉えようとすると実は難しいという話をしようと思います。
モータやエンジンのトルクは、一定ではない
前回、車やミニ四駆の加速度を求める方法を解説しました。
おさらいすると、ミニ四駆を例として、
加速度a={モータの出力トルクTm×ギヤ減速比ig/(タイヤ直径d/2)}/ミニ四駆の質量m
でしたね。
この計算では、モータトルクはタミヤのページに書かれているトルクを、最大値と最小値の平均値を使用していました。
実はモータは、常に一定のトルクを発生するというわけではないのです。
その詳しい仕組みは割愛しますが、停止時から動き始めた瞬間が最もトルクが高く、バッテリーの電圧で決まる最高回転数になると、トルクは小さくなる傾向にあります。
この、トルクが一定ではないというのは、車のエンジンも同様です。
エンジンの場合は、稀にエンジンカーブと呼ばれる、エンジンの回転数に対する出力とトルクのグラフを見かける事があるかもしれませんが、一定の値ではありません。
エンジン単体の場合、回転数が少ないとトルクが小さくなる傾向にあります。
これは、発進時に最も力が欲しい状態とは反します。
そこで、変速機が使われるのですね。
ともかく、今回解説する計算方法は、実際のモータやエンジンの特性全てを考慮しているわけではなく、複雑な事象を単純な条件に当てはめて計算するということです。
それでは今回はどのように計算するか。
それは後の章で解説します。
速度が高くなると、大きくなる抵抗もある
前回に続き、今回も結論のパートで、こう書かせてもらいました。
全ての抵抗は無視し、タイヤと路面との摩擦係数は1(滑らない)とする。
タイヤと路面との摩擦係数が1未満の値になる、つまり滑る可能性がある場合についての解説は、いずれできればと思います。
もう一つの、全ての抵抗は無視するという点についてです。
抵抗というのは色々な要素があるのですが、速度が速くなるにしたがって増える抵抗としては、例えば空気抵抗があります。
空気抵抗は、物体の形状によって変化する値、空気の状態で変わる値の他、空気の流れる速度(=車やミニ四駆が走る速度)も関わります。
今回は、これらの抵抗を無視します。
計算の考え方
計算の条件設定
先程解説した通り、正確なシミュレーションを行うためには、多くの事を考えなくてはなりません。
今回は、検討したい現象を、これまで導いてきた方法を使って簡単に捉えられないか、考えてみます。
まず、イメージですが、実際の速度の変化は、以下のようになります。

このグラフについて、速度の推移を示す線が、距離L=f(t)の形で表されるなら、計算できます。
ですが、現実的な速度の推移を一つの数式で表すのは難しいという事です。
そこで、このグラフを、以下のように簡単な現象として考えてみます。
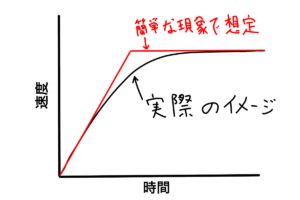
どのように考えたかというと、次の通りです。
- 全ての抵抗は無視し、タイヤと路面との摩擦係数は1(滑らない)とする。
- 最高速度の計算は、モータ回転数、ギヤ、タイヤ直径から導かれる速度とする。
- 加速度は、モータトルク、ギヤ、タイヤ直径、マシン質量から導かれる加速度を、最高速度に達するまで続ける(等加速度直線運動)ものとする。
つまり、スタートから最高速度に達するまでは、前回求めた加速度で加速していき、同様に求めた最高速度に達したら、最高速度で走り続ける、という、2つのパターンの組み合わせという事です。
最高速度の求め方については、以下のページをご覧ください。
加速度の求め方については、以下のページをご覧ください。
今回の問題を解く道筋
今回欲しい結果は、「スタートで出遅れたスピード重視のマシンが、いつこのマシンより速度が遅いが加速が速いマシンを追い越せるか」でしたね。
今後簡単に表記するため、加速重視のマシンをマシンA、スピード重視のマシンをマシンBとします。
ところで、どのような状態になれば、「マシンBがマシンAを追い越した」と判断できるでしょうか。
それは、スタートの位置が同じなので、Bの移動距離がAの移動距離よりも大きくなれば、追い越したと言えると思います。
よって、今回の問題では、「AとBの移動距離を計算する方法を導き、それぞれの移動距離を比べて、Bの移動距離の方が大きくなった時の時間を求める」という考え方で進めることになります。
頑張りましょう。
時間と速度の関係を表すグラフについて
先程示したグラフをもう一度見てみましょう。
このグラフは、横軸に時間、縦軸に速度を表しています。
このグラフについて、解説していきます。
まず、一定速度で走っている場合を考えましょう。
そもそも速度とは、「ある時間あたりに走った距離」という意味があるのでしたね。
同じ1秒の間に、走った距離が多い方が、速度が速いと言えると思います。
今、速度がV(mm/s)だったとします。
するとこのミニ四駆は、1秒後にはV(mm)、2秒後にはV(mm/s)×2(s)=V×2(mm)進むことになります。
同様に、t秒後には、V×t(mm)進むことになります。
この、距離=速度×時間というのは、実は小学生の時に習うかもしれません。
「みはじ」あるいは「はじき」の方法って聞いたことあると思います。覚えていませんか?
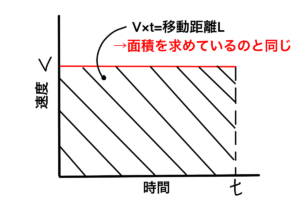
ここで、グラフをじっと見てみます。
V×tとは、何を示しているでしょう。
いま、横軸に時間、縦軸に速度をとっているグラフです。
V×tは、Vとtで示される範囲の面積を求めることになりそうですね。
結果的に、縦軸に速度V、横軸に時間tを取ったグラフ(V-tグラフと呼ばれます)で示された範囲の面積を求めることで、移動距離Lが求まります。
これは、高校数学でいうところの「積分」を行っていることと同様となります。
ある一瞬Vで走っている時の距離の変化をt秒間積み重ねると、全体の移動距離Lになるということですね。
難しいので、「積分ってグラフで囲まれた範囲の面積を求めること」と思っていただければ十分です。
では次に、一定の加速度で加速しているブラフを見てみましょう。
いま、加速度a(mm/s^2)で加速している状態です。
つまり、速度0からスタートしたら、1秒後にはa(mm/s)に、2秒後にはa×2(mm/s)に、t秒後にはa×t(mm/s)になるような加速度で走っているということです。
さて、この一定の加速度で走って、t秒後にV(mm/s)になるマシンは、どのくらいの距離を走ることになるのでしょう。
先程分かった通り、移動距離Lは、t秒間、速度のグラフで表される範囲の面積を求めることになるのでしたね。
今回は長方形ではなく、三角形の形をしています。
つまり、面積を求めるには、三角形の面積を求める公式を使って、
L=(1/2)×V×t
となります。
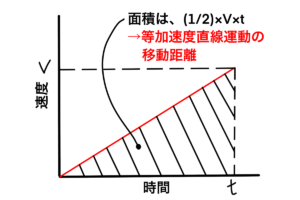
なぜ?
移動距離は面積を求めることだから…では、あまり納得しないでしょう。
今回の同じ加速度aで走行し、t秒間にVになる場合というのは、平均速度を簡単に求める事ができます。
速度0からVまで一定に速度が上がっていく場合、平均速度は(1/2)×Vですよね。
なぜなら平均値を求めようとすると(V+0)/2だからです。
よって、L=(1/2)×V×tです。
そして先程書いたのですが、一定の加速度であれば、V=a×tでしたよね。
よって
L=(1/2)×V×t=(1/2)×a×t^2
となり、加速度aを使っても移動距離Lを計算することができます。
結果ですが、縦軸に速度V、横軸に時間tを取ったV-tグラフは、t秒間グラフが示す範囲の面積を求めると、移動距離Lを求めることになります。
これ、超高確率で高校物理学のテストに出ますし、グラフに移動距離が現れることを理解していればかなり問題が解けるようになります。
マシンの移動距離の計算
計算に必要な式の整理
さて、移動距離の計算に必要な式は揃いました。
後は「マシンBがマシンAを追い越した時」を判定する式を作れば良いですね。
「今回の問題を解く道筋」の節でも述べた通り、同じ位置からスタートするので、「AとBの移動距離を計算する方法を導き、それぞれの移動距離を比べて、Bの移動距離の方が大きくなった時の時間を求める」事で、マシンBが追い越したかどうかを判断することができます。
順番に式を整理しましょう。
計算に必要な式まとめ。
スタート時速度0で、等加速度で走る場合の移動距離L1
L1=(1/2)×a×t^2
一定速度で走る場合の移動距離L2
L2=V×t
最高速度Vに達するまでの時間tc
V=a×tcより、
tc=V/a
スタート時速度0で、スタート後等加速度で走り、tc秒後に最高速度Vに達した後は速度Vで走る場合の移動距離L
L=L1+L2
L=(1/2)×a×tc^2 + V×(t-tc)
※一定速度Vで走るのは、Vになった後です。Vになるためにtc秒かかるので、一定速度Vで走っている時間は、全体の時間t秒からtc秒引いた時間となります。
加速度aは、ミニ四駆のモータトルクTm、ギヤの減速比ig、タイヤ直径d、マシンの質量mを使い、以下の通りです。
a={(Tm×ig)/(d/2)}/m
ミニ四駆の最高速度Vは、モータ回転数nm、ギヤの減速比ig、タイヤ直径dを使い、以下の通りです。
V=(nm/ig)×d×π
ちなみにExcelでは、円周率を使う関数 =PI()と入力すると、3.14159265358979と、小数点以下14桁を使うようです。
もうひとつちなみに、私が普段プライベートで使っている表計算ソフトのNumbersでも、PI()=3.14159265358979でした。
「マシンBがマシンAを追い越した」を、ちょっとでも簡単に計算する方法
さて、何度も繰り返しますが、マシンBがマシンAを追い越すためには、Bの走行距離Lbが、Aの走行距離Laより大きくなれば良いのですよね。
ここで、マシンが最高速度に達するまでの時間をtca、同様にマシンBはtcbとしますが、スタートからtcb秒後には、2台のマシンはどういう関係になるでしょうか。
まずは、tcb秒後に既にマシンBが追い越しているのかいないのかを計算しておくと良いと思います。
その方法は、マシンAとマシンB、それぞれtcb秒後の移動距離を求めて、比較しましょう。
この比較により、次のパターンに別れます。
- もしマシンBがマシンAを追い越している場合、二つのマシンの移動距離よりLa=Lbとなるように方程式を組みます。その式をt=の形に置き換えて、tを解く事で追い抜く時間を求めましょう。ちなみに、t<tcaの時は、マシンBよりマシンAの方が加速度が大きいので、マシンAは絶対に追い越されません。tca≦t≦tcbの範囲で考えましょう。
- もしマシンBがマシンAを追い越していない場合は、次に説明する方法で考えると少し楽です。
もしマシンBがまだ追い越していない場合、tcb秒後の2台のマシンは、次のような関係になります。
tcb秒後にそれぞれのマシンが進んだ距離は、先程の追い越したかどうかの判定で計算していますね。
その時、マシンAが進んだ距離Laから、マシンBが進んだ距離Lbを引きます。
そうすると、マシンAとマシンBの離れている距離Ls=Lb-Laが求まります。
次に、2台のマシンは共に、一定速度で走っている状態です。
マシンAの速度はVa、マシンBの速度はVbで、Va<Vbです。
この時、マシンAから見ると、マシンBは速度の差Vs=Vb-Vaの速度で近づいているように見えます。これを「相対速度」と言います。
この相対速度Vsで、距離Lsが0になる時間tsを求めます。
つまり、ts=Ls/Vsであり、マシンBが一定速度になったts秒後に追い越したと言えます。
最終的に、マシンBがマシンAを追い越した時間t=tcb+ts秒と言えます。
実際の計算
ところで、計算って結構めんどくさいですよね。
今のところは普通の電卓でも計算できますが、高校生までのほとんどの人が持っていなく、工学系の大学生になるとほぼ全員持つことになる、便利なアイテムがあります。
それが、関数電卓です。
私が今実際に使っているのが、カシオ FX-JP500です。
カシオの関数電卓は、分数などの表記が数学でいつも通り書くその見た目で表示できるので、とても分かりやすいです。
私が大学入学の時に買ったのは、旧モデルのカシオ FX-913ESです。
もちろんその当時から自然表示機能も含まれていますし、高校の頃あれだけ苦労した三角関数や定積分なども含まれており、大学で初めて使った時は「チートアイテムきたわwww」と思いました。
ちなみに、工学系などの理系の大学では、テストの時に使うことも珍しくありません。
なので大学入学説明で「関数電卓を買ってください」と言われている場合は、絶対に買ってください。
また、大学や学科によっては、グラフ表示やプログラミング機能が付いているものを使うこともあるかもしれません。
また、行列計算をしたり、分布計算をするなどの場合、上記関数電卓の上位モデルを買う必要がありますが、一般的な関数計算であればFX-JP500で不足することは無いと思います。
現に私も、機械設計の仕事において、行列の計算は全く使っていません。
行列の計算が必要になった場合はExcelで、と割り切っています。
使用状況により、必要なもの・使いやすいものを買いましょう。
マシンの条件
マシンAについて。
モータトルクTma:トルクチューン2モータとして、1.8(N・mm)
モータ回転数nma:トルクチューン2モータとして、13500(r/m)=225(r/s)
ギヤ減速比iga:超速ギヤとして、3.5
※なぜ、加速重視マシンなのに超速ギヤか。それは、トルクチューン2モータに標準ギヤだと遅すぎたからです。
タイヤ直径da:小径タイヤとして、24(mm)
マシン質量m:120(g)
最高速度Va=(Tma/iga)×da×π
Va=4847(mm/s)
加速度aa=Tma×iga/{(da/2)×m}
aa=4375(mm/s^2)
最高速度に達するまでの時間tca
tca=Va/aa
tca=1.11(s)
マシンBについて。
モータトルクTmb:レブチューン2モータとして、1.35(N・mm)
モータ回転数nmb:レブチューン2モータとして、14300(r/m)=238.3(r/s)
ギヤ減速比igb:超速ギヤとして、3.5
タイヤ直径db:大径タイヤとして、31(mm)
マシン質量m:120(g)(マシンAと同じ)
最高速度Vb=(Tmb/igb)×db×π
Vb=6631.8(mm/s)
加速度aa=Tmb×igb/{(db/2)×m}
ab=2540(mm/s^2)
最高速度に達するまでの時間tcb
tcb=Vb/ab
tcb=2.61(s)
マシンBが最高速度に達した時の移動距離
マシンBが最高速度に達するまでの時間tcb=2.61(s)
tcb時点でのマシンAの移動距離La
La=(1/2)×aa×tca^2 + V×(tcb-tca)
La=(1/2)×4375×1.11^2 + 4847×(2.61-1.11)
La=9965.7(mm)
tcb時点でのマシンBの移動距離Lb
Lb=(1/2)×ab×tcb^2
La=(1/2)×2540×2.61^2
La=8651.4(mm)
マシンBが最高速度に達した時、マシンBがLs=La-Lb=1314.3mmの差を埋めようと頑張る状態になりましたね。
マシンBが最高速度に達してから追い越すまでの時間
これは先程「『マシンBがマシンAを追い越した』をちょっとでも簡単に計算する方法」で解説の通り、距離の差Ls=La-Lb=1314.3mmを、速度の差(相対速度)Ls=Vb-Va=6631.8-4847=1784.8(mm/s)で走る時の時間となります。
よってマシンBが最高速度に達してから追い越すまでの時間tsは、
ts=Ls/Vs
ts=1314.3/1784.8
ts=0.74(s)
同時にスタートし、マシンBがマシンAを追い越すまでの時間
マシンBが最高速度に達してから追い越すまでの時間tsがわかりましたので、マシンBが最高速度に達するまでの時間と足すことで、マシンBがマシンAを追い越すまでの全体の時間が求まります。
t=tcb+ts
t=2.61+0.74
t=3.35(s)
どうでしょうか。等速、等加速、それぞれでの移動距離を求める式を組み合わせて、スタートで出遅れた最高速度重視のマシンが、スタートで有利だった加速重視のマシンを追い越すまでの時間を求めることができました。
色々なパターンの計算結果をグラフで見てみる
これで、ある時間tにおける、マシンの移動距離を求めることができました。
最後にお楽しみとして、同じように以下の4つのマシンで同時にスタートした時の速度の変化や移動距離の変化をグラフにしてみましょう。
以下の4つのマシンの共通事項
レブチューン2モータ
質量0.12kg
マシンA
減速比:標準ギヤとして5
タイヤ直径:小径タイヤとして24(mm)
マシンB
減速比:標準ギヤとして5
タイヤ直径:大径タイヤとして31(mm)
マシンC
減速比:超速ギヤとして3.5
タイヤ直径:小径タイヤとして31(mm)
マシンD
減速比:超速ギヤとして3.5
タイヤ直径:大径タイヤとして31(mm)
マシンAが最も加速重視で、マシンDが最も最高速度重視、マシンBとマシンCは中間のセッティングとなっています。
計算方法は、これまでと同様なので省略します。
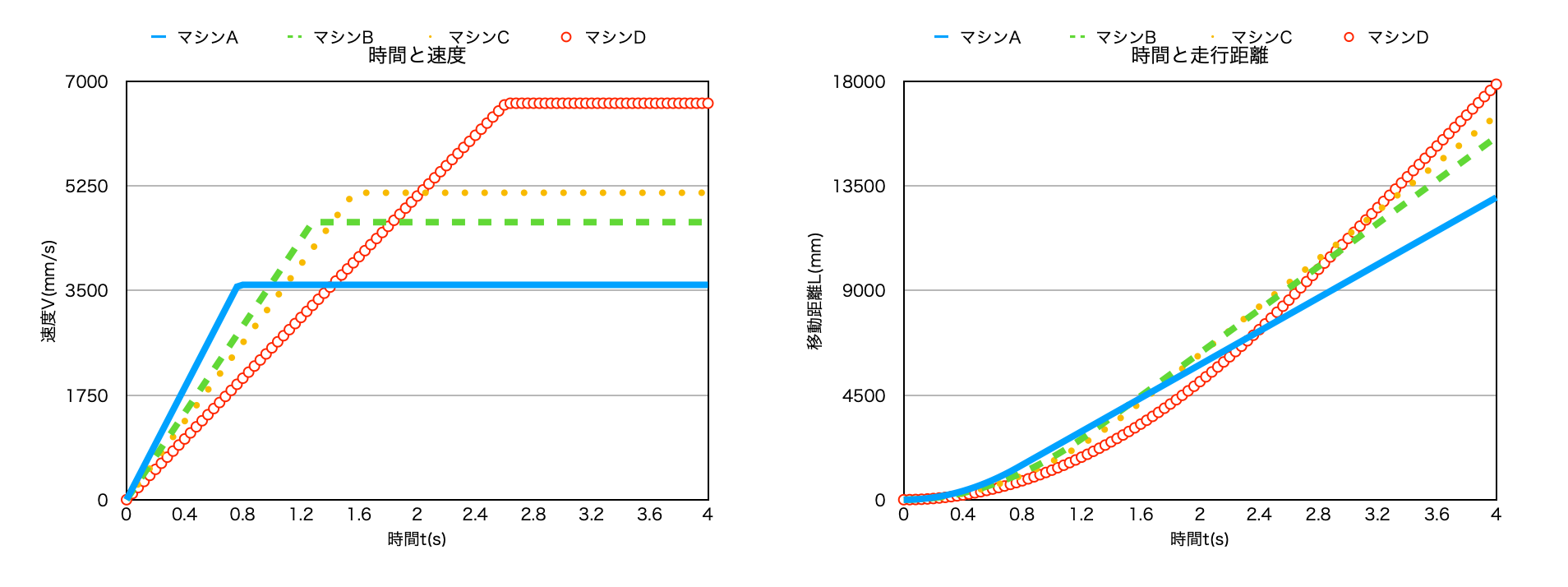
結果をグラフにまとめましたので、ご覧ください。
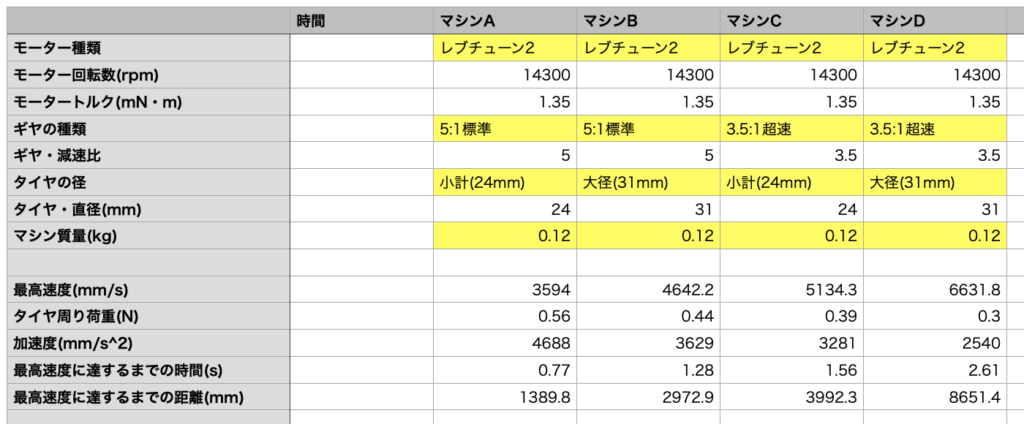
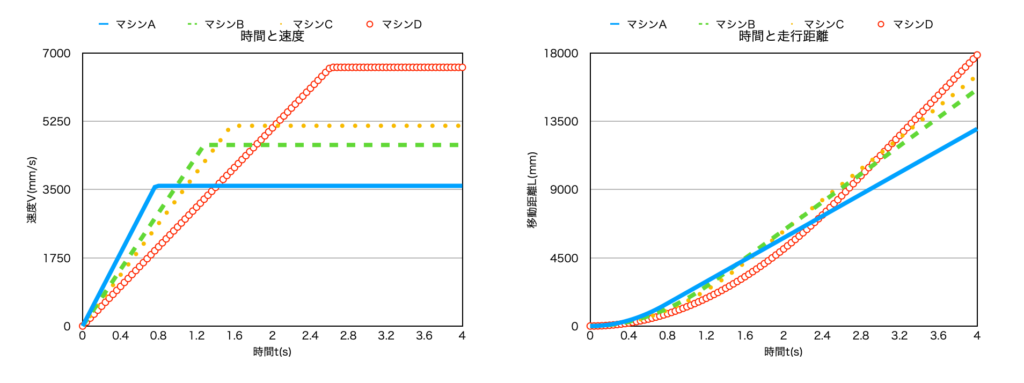
今回の結果では、A→B→C→Dの順で、Aが加速重視、Dが最高速度重視のセッティングであることが分かると思います。
マシンDがマシンAを追い越した時間は、スタートから約2.4秒後でした。
また、移動距離のグラフを見ると、中間セッティングであるマシンBやマシンCが一位になっているタイミングもあります。
つまり、コースによって加速、最高速を調整することが重要で、どのバランスがそのコースにとって速くなるのかを見極める必要があることが言えると思います。
(コーナーが多いコースなどでは、マシンが減速し、マシンDが一番遅い可能性もあります)
超速ギヤを使っておけば良いとは言えないのです。コースによって変わるのです。
ちなみに、今回の検証で、一つ発見があります。
それは、標準ギヤと大径タイヤのマシンBと、超速ギヤと小径タイヤのマシンCが、最高速度と加速の性能がほぼ同じということです。
もしこの速度や加速力を目指そうとセッティングする時、どちらもほぼ最高速と加速性能が同じなのですが、一般的に小径タイヤの方が安定性が高くなる傾向にあるので、超速ギヤと小径タイヤの組み合わせにすると、同じような性能で安定性を高められることができるということになります。
計算してみて良かったですね。
まとめ
もう一度今回の結論を書きます。
計算条件
直線のコースとする。(コーナーによる減速を考えない、直線運動)
全ての抵抗は無視し、タイヤと路面との摩擦係数は1(滑らない)とする。
最高速度の計算は、モータ回転数、ギヤ、タイヤ直径から導かれる速度とする。
加速度は、モータトルク、ギヤ、タイヤ直径、マシン質量から加速度求め、最高速度に達するまで一定の加速度を保つ(等加速度直線運動)ものとする。
計算方法
移動距離L=加速中に移動した距離L1+等速で移動した距離L2
スタートからの時間をt、スタートから最高速度に達するまでの時間をtcとすると、
L=(1/2)×V×t=(1/2)×a×t^2 (但し、t < tc)
L=(1/2)×V×tc + V×(t-tc) (但し、t ≧ tc)
加速重視マシンの移動距離Laより、スピード重視マシンの移動距離Lbが大きくなった時の時間tが、追い越した時間となる。
今回、マシンが速度0から、モータなどの情報を基に計算した加速度で加速し、同じくモータなどから計算した最高速度で走り続けた場合の移動距離を求めることで、スピード重視のマシンがどのくらいで加速重視のマシンを追い越すかを検証してみました。
もちろんコースによってベストなセッティングはさまざまですが、加速重視にするかスピード重視にするかバランスを取るかの参考にして頂ければと思います。
さて、このブログではここまで、車やミニ四駆の速度、加速度、移動距離という、物体の運動についての基礎であり重要な事項について解説してきました。
もちろんこれからも物理学に関する記事を書いていきますが、ここからは時々、以下の内容も書いていきたいと思います。
- オフィス系ソフトのヒントになるような記事。
- 車やバイクに関する日記(まさに、ブログ)。
今回、グラフを作成するにあたり表計算ソフトを使いました。
一体どうやって速度や移動距離のグラフを書いたのか、計算したのか。
そのような参考を示せたらなと思います。
また、不明点やこんなことを知りたいということがありましたら、コメントやお問い合わせフォームからメッセージをください。
※しばらくは物理学の中でも、力学の分野で記事を進めていこうと思います。
それでは、次回もお楽しみに。


コメント