こんにちは。ジェノンです。
かなり久しぶりの更新になってしまいました。お久しぶりです。
前回より、ミニ四駆のコースアウトについて考えてみようという事で、記事を書いています。
前回はコースアウトの序章として、力のモーメントについて解説しました。
今回は、コーナーでのコースアウトについて、コーナリング時に働く力を考えたいと思います。
それでは、よろしくお願いします。
この記事について
この記事で分かること
- コーナリング時に働く力について。
こんな人に向けて書いています。
- ミニ四駆がコーナーでコースアウトして困っているので、ヒントが欲しい。
記事の対象:高校生以上
この記事の結論
ミニ四駆や車がコーナリングする運動を、円運動の一部と考えると、車体にはカーブ内側に向かう力が必要である(向心力)。
一方向心力が外部から与えられた時、向心力を与える物から見ると、車体は外側に力を受けているように見える(遠心力)。
コーナリング時に働く力について
車体のどこに力が働くと考えるか
コーナリング時に働く力について考えます。
コーナーでコースアウトするという事は、ストレートを走っている時とは違う力が働いていると考えられると思います。
まずは、その力がどこに働くのかを解説します。
ところで、今回の記事からは、「車体」という表現を使います。
というのは、これまでミニ四駆は「マシン」、車は「車」というように、呼び分けていました。
しかし、ミニ四駆も車も共通する内容が多いので、共通する内容の場合はひとまとめに「車体」と呼ぶことにします。
それでは、コーナリング時に車体にどのような力が働くかを考えます。
まずは力の大きさではなく、力が働く場所を考えましょう。
以前、力Fと物体の質量mと加速度aとに、次の関係がある事を紹介しました。
F=m×a(ニュートンの運動方程式)
ミニ四駆の加速度を求める時などに利用しましたね。
その時は、何気なくミニ四駆全体の質量を使っていましたが、よく考えればミニ四駆というのは多くの部品で構成されていますよね。
例えばモータ、ギヤ、シャフト、ボディ、シャーシ…。
それら一つ一つにも、質量があります。
これらの質量は考えずに、全体の質量を使って考えていました。これで良いのでしょうか。
実は、マシン全体の運動を考えようとする時は、マシン全体の質量で計算して良いです。
厳密に言えば、それぞれの部品について、
F=m×a
が当てはまります。
それを、部品1の時にF1=m1×a、部品2ではF2=m2×a、…と全部計算します。
ちなみに、全ての部品が同じように加速していくので、aは全て同じ値になりますね。
これら部品それぞれで計算したとして、これを全部足すと
ΣFi=(Σmi) ×a
となるのですが、Fおよびmを全て足すと、結局マシン全体で考えた時のFとmになります。
※全ての部品が同じように動くので、aが等しく、各部品の質量miを全て足すと全体の質量mとなるので、右辺が同じなら左辺も同じ、ということで、各部品に働く力Fiを全て足すと、全体に働く力Fと等しくなると言うことですね。
それで、話を戻しますが、車体全体で考えた時、どの位置に加速させるための力Fが働くのかという事です。
先ほど解説の通り、実際には各部品ごとに力が働いています。
もっと言うと、各部品を構成している原子毎に力が働いています。
それをぜーんぶまとめると、全体の重心位置に力が働いていると扱うことができます。
これを「質点系の力学」と言います。
実際には部品1個ずつ、原子1個ずつに働いた力と質量を積分すると、全体の重心位置に力が働いた状態と同じであると言う事です。
ちょっと頭が痛くなりそうなので、もう一度結論だけまとめると、運動する物体に働く力は、重心位置に働くと考えられます。
いくつかの部品が組み合わされた物でも、その物全体の重心位置に力が働くと考える事ができます。
コーナリング中にどうやって力を受けているか
ストレートでは安定して走ることができるのに、コーナーでマシンが転倒してコースアウトしてしまう原因。
それは、コーナリング中に、マシンを転倒させるような力を受けていて、それに耐えきれていないからです。
マシンが加速する場合については、タイヤで力を発生させていますが、コーナリング中に力を受けるとはどう言う事でしょうか。考えてみましょう。
ちょっとだけ脱線しますが、車が曲がるためには、ハンドルを回転してタイヤの向きを変えれば曲がりますよね。
つまり、曲がるためには、進むのと同じく、タイヤが路面に対してある力を与えて、その反作用として曲がる力を得ています。
難しい事は今回は省略しますが、それまで真っ直ぐに走っていた車体が例えば右に曲がる時、それは右方向にも加速度が与えられた状態と言えます。
そしてその発生源は、車の場合はタイヤです。
ミニ四駆の場合はやや複雑な状態となっていますが、ローラーがフェンスに当たって反発力を得て、その力はシャーシを通してマシン全体に伝えられているイメージです。
それで、ミニ四駆の場合ローラーがフェンスに当たり、フェンスから右方向に進む力を得て曲がろうとしています。
この瞬間、車体重心は真っ直ぐ進もうとしている(横方向に力が働いていない)という状況になります。
この状況は、逆にローラーから見ると、「車体を右側に押そうと思うと、車体から左向きに力を受けている」と言うことに注意してください。(遠心力とも言われます)
と言うことで、車体重心にどのくらいの大きさの力を受けているか。
それは、車体がどのくらい右方向に力を得ているかが分かれば、その逆方向といえます。
コーナリング中にどのくらいの力を受けているか
いよいよ、コーナリング中に受ける力について考えます。
引き続き、車体は右方向に曲がろうとしているとして解説します。
先ほど解説した通り、車体が右方向に曲がろうとしていると言うのは、右方向に加速度を与えられていると考えることができます。
それまで真っ直ぐにしか進んでいない(右方向の速度が0)ものが、ある速度で右方向に進んでいる、つまり右方向への速度が上がったということですね。
それはまさに、「右方向に加速した」と言えると思います。
この右方向への加速度が分かれば、F=m×aにより、力Fが分かりそうですね。
頑張りましょう。
図のように、速度Vで走っていた車体が、コーナーの曲率半径Rで曲がったとします。
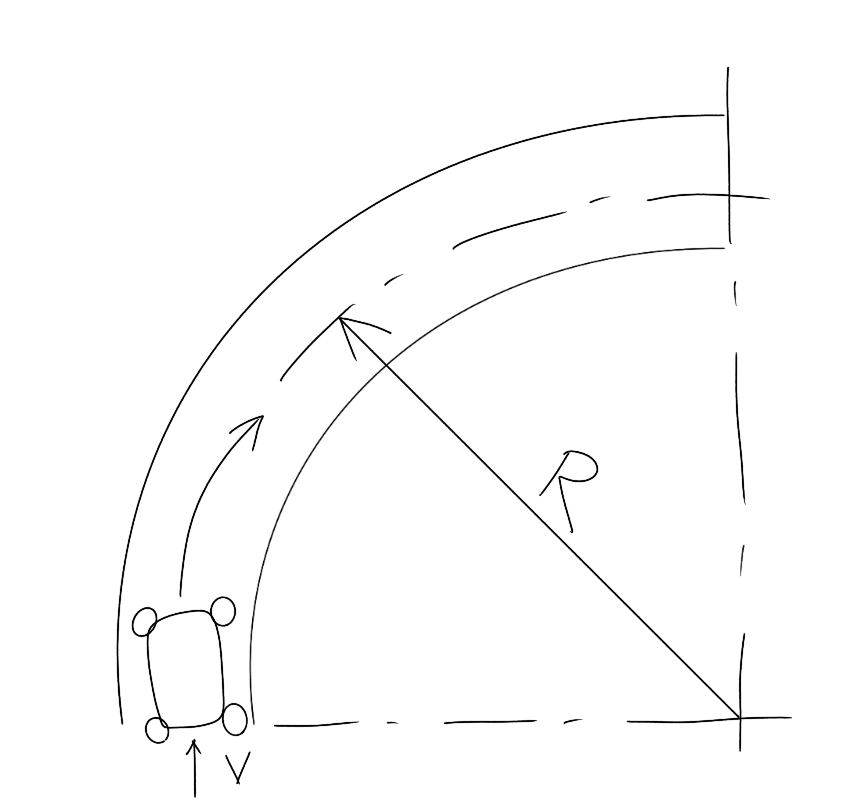
この時の右方向への加速度を求めてみたいと思います。
コーナリングの一部分のみを切り出すと複雑ですが、もし右旋回を続けると、ちょうど1周回りますよね。
このような状況になる良い例題があります。
それが、円運動の加速度を求める問題です。
この円運動の加速度についてですが、分かりやすく解説しているブログがありましたので、そちらを参考にしていただければと思います。
こちらの記事のタイトル、そのまんまですね。
向心力
向心力
http://www.wakariyasui.sakura.ne.jp/p/mech/enn/kousinn.html
動くイラストを使った解説、わかりやすいですね…。
円運動を求めるポイントとしては、時間当たりにどのくらいの距離を進むかという単純な速度vだけでなく、時間当たりにどのくらいの角度で回るかを表す、角速度ω[rad/s]を使う事で、表しやすくなります。
角度の単位、[rad]は「ラジアン」で、360[°]=2π[rad]です。
それで、先ほどのブログで得られるのですが、右回りに回る物体には、右方向に、正確には旋回する半径の中心方向に加速度aを発生します。
そのaの大きさは、
a=rω^2=v^2/r
となります。
よって、コーナーの円弧半径がrで、その時のマシン速度がvの時、加速度aは
a=v^2/r
となります。
車の場合、ここで求めた力を発生しきれない場合、つまりタイヤが発生できる限界の力を超えている場合、タイヤはスリップし、曲がりきれなくなります。
しかし、ミニ四駆の場合はローラーがフェンスに当たっているため、強制的に向心力を与えられることになります。
その向心力に耐えきれなくなった時、ミニ四駆はコースアウトします。
では、どのように耐えきれなくなったらコースアウトするのか。
それは、次回説明しようと思います。
まとめ
今回は、車体がコーナリングする時に、どのような力が発生するかを解説しました。
最終的にミニ四駆がコースアウトするかどうかは、この力を受けた状態であっても車体が安定する状態になるかどうかが重要です。
次回は、コーナリング時の安定度を解説したいと思います。
次回もお楽しみに。

コメント