こんにちは。ジェノンです。
このブログではこれまで、車やミニ四駆の速度、加速度について解説してきました。
速度や加速度を決める要因が分かれば、速いミニ四駆を作りやすいかもしれませんね。
しかし、ミニ四駆については、ただマシンを速くするだけでは勝てない事は、ミニ四駆をやっている方であれば理解できると思います。
そう、いくら速くても、コースアウトしてしまっては失格してしまうからです。
そこで今回から、ミニ四駆のコースアウトについて考えたいと思います。
コースアウトについての序章として、今回は特にコーナーでのコースアウトに大きく関わる、力のモーメントについて解説します。
よろしくお願いします。
この記事について
この記事で分かること
- 力のモーメントについての基本。
こんな人に向けて書いています
- ミニ四駆がコースアウトして困っているので、ヒントが欲しい。
記事の対象:中学生以上
この記事の結論
ミニ四駆がコーナーでコースアウトする場合、力のモーメントが関わる場合がある。
力のモーメントMは、次のように表される。
力のモーメントM=力F×回転支点から力までの長さL
力のモーメントについて
モーメントとは何か
これからミニ四駆がコーナーでコースアウトする場合に大きく関わる、力のモーメントについて解説していきます。
とはいえ、物理学を学んでいない人にとって、速度や加速度はまだしも、力のモーメントと言われてもピンと来ないと思うので、まずは力のモーメントとは何かをまとめます。
モーメントを日本語に訳そうとすると、ちょっと難しいです。
単純な英語としては、「瞬間の」という意味があります。(Twitterにも、モーメントってありますよね)
ただ、力のモーメントという言葉では、あまり「瞬間」という意味は強調されていないと思います。
物理学における力のモーメントとは、物体が回転しようとする力の事だと捉えていただければ十分です。
力のモーメントの求め方
それでは、物体が回転しようとする力を求めようと思います。
といっても、実は多くの方が、小学校で習っている事が出てくるのです。
力のモーメントM=回転方向に対して垂直方向の力F×回転中心から力までの半径方向距離R
※一般的には上記の通り「力のモーメント」と呼ばれるのですが、今後この記事ではイメージを持ちやすくするために「回転モーメント」という表現をさせてもらっています。
何が小学校でも習う事なのかというと、回転モーメントは、力×回転する腕の長さなのです。
似たような事、理科で出てきませんでしたか。
そう、てこの原理です。
てこの原理は、回転支点から遠いところで力をかけると、回転支点に近いものに大きな力を与えられるというような事でしたね。
このてこの原理を使ったものの例として、空き缶潰しやバール、そして公園にあるシーソーが挙げられると思います。
シーソーは、仮に同じ体重の人が乗っても、乗る場所で相手を持ち上げられるか、逆に自分が持ち上がるか変わるのですよね。
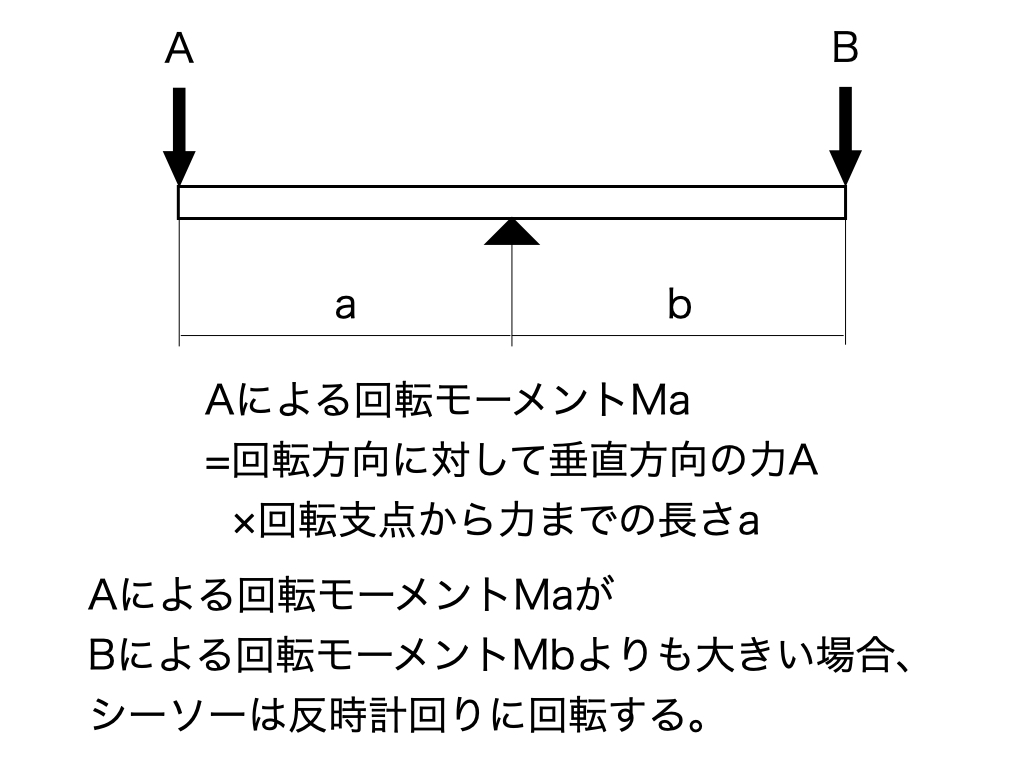
あれも実は、体重(下向きの力)×座る位置の距離(回転中心からの距離)が大きくなる方向に回転します。
シーソー全体の回転する力がどちら向きに大きくなるかで、片方が上がったり下がったりしているのです。
この力×回転中心からの距離というのは、以前の記事でも出てきました。
それは、車やミニ四駆のタイヤが回転する事で発生する、前に進もうとする力を求めるところです。
その記事はこちら。
回転モーメントM=力F×回転中心から力までの半径長さR
タイヤ周りについては、Mはタイヤの回転トルクT、Rはタイヤ半径rとなります。
よって
T=F×r
F=T/r
となったのですね。
例題
先程解説した回転モーメントに関する例題を解いてみましょう。
図のように、シーソーにA、Bが座っている。但し、重力加速度はg=9.81(m/s^2)とする。また、シーソーの重さは無視する。
問1)Aによる反時計回りの回転モーメントを求めよ。
問2)Bによる時計回りの回転モーメントを求めよ。
問3)図のシーソーは、どちら回りに回転するか。
問4)ここに、重りCを乗せて、シーソーがつり合う(シーソーの回転モーメントが0となる)ようにしたい。Cはどこに置けば良いか。

解答例
問1)
Aによる回転モーメントを求める問題です。
モーメントM=力F×回転中心から力までの半径方向距離Rです。
ここで、Aによる下向きの力Faを求めます。
Aは重さにより、下向きに力を与えます。
ところで、Aが50(kg)と言っていますが、これは力の単位ではありません。質量(重さ)の単位です。
地球上において、ある質量が下向きに落ちる時の力は、地球上であれば問題文より重力加速度g=9.81(m/s^2)を掛け算する事になります。
具体的にはAによる下向きの力Fa=A×g
=50×9.81
=490.5(kg×m/s^2 = N)
力の単位、ニュートン(N)になりましたね。
以上より、Aによる反時計回りの回転モーメントMaは、
Ma=Fa×a
=490.5×2
=981(N・m)
答え:981(N・m)
問2)
Aと同様に、時計回りの回転モーメントMbを求められます。
Mb=Fb×b
=B×g×b
=60×9.81×1.3
=765.18(N・m)
答え:765.18(N・m)
問3)
MaとMb、大きい方向に回転します。
Ma=981(N・m) > Mb=765.18(N・m)
答え:Maの回転モーメントの方が大きいので、シーソーはAの力の方向、つまり反時計回りに回転します。
問4)
重りCを足す事によって、シーソー全体の回転モーメントを0にする問題です。
これは、Cを足す事によって、反時計回りのモーメントと時計回りのモーメントの差を0にする事になります。
今、
Ma=981(N・m)
Mb=765.18(N・m)
でした。
二つの差を取る事で、Mbにあとどのくらい時計回りのモーメントを足す事で、反時計回りと時計回りのモーメントを等しくする事ができるか求められます。
モーメントの差(=発生させたいモーメント)Mc=Ma-Mb
=981-765.18
=215.82(N・m)
モーメントM=力F×回転中心から力までの半径方向距離Rより、
Cの設置位置c=(発生させたいモーメントMc)/(Cによる力Fc)
=215.82/(20×9.81)
=1.1(m)
答え:回転支点から1.1m右の位置にCを設置することで、シーソーは回転のモーメントのつり合いが取れ、回転しなくなります。
ちなみに、問題を一つずつ解いているので重力加速度を掛け算している状態で求めていますが、モーメントの差を求める時は、重力加速度が同じであれば、掛け算していなくても同じように求められます。
Ma=Mb+Mc
Fa×g×a = Fb×g×b + Fc×g×c
↑両辺にgが掛け算されているので、両辺をgで割り算すると、
Fa×a=Fb×b+Fc×c
c=(Fa×a – Fb×b)/Fc
=(50×2 – 60×1.3)/20
=1.1(m)
このように、重力加速度を都度掛け算するのではなく、一度各値を記号のまま整理する事で、計算が簡単になることは多くあります。
もちろん関数電卓や表計算ソフトなどで計算するのであれば、あまり手間は変わらないかと思います。
しかし、例えば高校のテストでは電卓は使えませんので、記号のまま整理してあらかじめ計算を簡単にするテクニックはとても重要です。
まとめ
今回は、ミニ四駆のコースアウトについての序章として、特にコーナーでのコースアウトに大きく関わる、力のモーメント(回転モーメント)について解説しました。
結論を復習します。
ミニ四駆がコーナーでコースアウトする場合、力のモーメントが関わる場合がある。
力のモーメントMは、次のように表される。
力のモーメントM=力F×回転支点から力までの長さL
というわけで、次回はコーナーにおけるミニ四駆のコースアウトについて書く予定です。
お楽しみに。

コメント